Cautarea binara pentru olimpiada in C++
Ce este căutarea binară?
Să zicem că ai un vector a[] cu n elemente crescătoare. Căutarea binară este un algoritm eficient care determină dacă orice număr x apare sau nu în şir (în caz afirmativ putem afla poziția, câte elemente egale cu x sunt etc.).
Aproape în fiecare an, la mai toate clasele, apar probleme cu căutarea binară, atât la OJI, cât şi la ONI[1].
ATENȚIE! Formulele nu trebuie reținute, ci deduse.
Cuprinsul lecției
Deducerea algoritmului de căutare binară
Să luăm următorul enunț ca exemplu:
CERINȚĂ. Se dau următoarele date de intrare: un număr natural n, n numere naturale în ordine crescătoare (a[i] ≤ a[i + 1], pentru orice 1 ≤ i < n) care constituie un vector (a[]), un număr natural q şi q numere naturale. Pentru fiecare dintre cele q numere aflați dacă se află în vectorul a[].
DATELE DE INTRARE au fost descrise anterior.
DATELE DE IEŞIRE. Vor exista q răspunsuri de "DA" sau "NU", pentru fiecare întrebare.
Algoritmul naiv (NERECOMANDAT!)
Parcurgem toate elementele în ordine până când găsim elementele cerute. Dacă am ajuns la i == n şi, cu toate acestea, nu am găsit numărul, atunci acesta nu există în vector. Complexitatea O(q * n). Soluția aceasta nu este bună în cazul în care n şi q sunt foarte mari, de exemplu n = q = 1.000.000, care iese din aproape orice limită de timp.
pentru (i de la 1 la q) {
citim x;
bool am_găsit = false;
pentru(j de la 1 la n) {
dacă(x este egal cu a[j]) {
am_găsit = true;
}
}
dacă(am_găsit) afişez "DA";
altfel afişez "NU";
}
Algoritmul de căutare binară
Cheia algoritmului este că şirul este crescător. Asta înseamnă că dacă un număr a[i] < nr de căutat, atunci toate a[j] cu j ≤ i sunt < nr de căutat; invers pentru numerele mai mari.
Cea mai eficientă abordare este să luăm numărul din mijlocul şirului, adică a[n / 2]. Dacă numărul este mai mic decât ce căutăm, atunci din start tăiem primii n / 2 termeni, şi reciproc şi pentru numerele mai mari. Continuăm tot aşa, tăiând jumătate din cât a rămas. Dacă găsim la vreun pas numărul, ne oprim şi afişăm corespunzător. Dacă ajungem la situația în care nu mai putem tăia în jumătate şirul nostru (adică am tot tăiat până când a rămas un singur element), ne oprim şi afişăm că elementul nu este în sir.
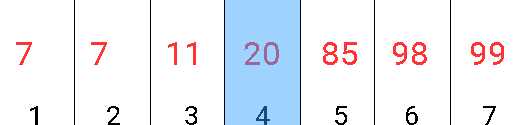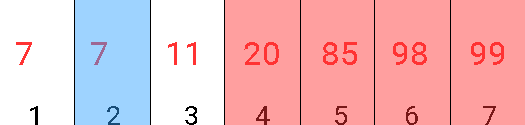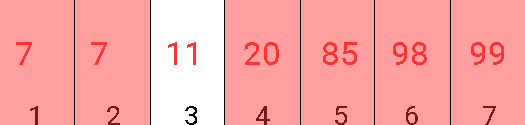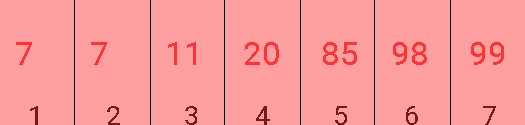
Iată o simulare pentru şirul a[] = {7, 7, 11, 20, 85, 98, 99} şi elementul de căutat x = 85:

În loc să facem 5 verificări cu metoda naivă, facem doar 3, aproape jumătate (în cazul acesta).
Iată o simulare pentru acelaşi şir, dar cu x = 19:
Complexitatea soluției este O(log2 n) pentru fiecare căutare — un număr extrem de mic raportat la valori mari ale lui n. Ca idee, dacă n = 1.000.000, log2 n = 19.93(adică se fac 20 de comparații în cel mai rău caz, în loc de 1.000.000).
OK, am înțeles algoritmul. Dar cum "tăiem" şirul? Vom considera doi indici, st şi dr, cu valorile inițiale st = 1 şi dr = n. La fiecare pas, vom realiza căutarea între aceşti indici. Dacă elementul din mijloc, (st + dr) / 2, este mai mare decât ce căutăm noi, atunci eliminăm tot ce este ≤ (st + dr) / 2, adică dr = ((st + dr) / 2) - 1;. La fel şi invers. Iată codul final:
#include <iostream>
#define MAX 100
using namespace std;
int n, a[MAX + 1], q, x;
int main()
{
//Citire. Ştim clar că numerele şirului
//a[] sunt crescătoare (din enunț)
cin>>n;
for(int i = 1; i <= n; i++) {
cin>>a[i];
}
cin>>q;
for(int i = 1; i <= q; i++) {
cin>>x;
int st = 1, dr = n;
int mij; //În loc să tot scriem (st + dr) / 2
//vom calcula valoarea în variabila mij
bool found = false;
while(found == false && st <= dr) { //condiția că mai putem împărți şirul
mij = (st + dr) / 2;
if(x == a[mij]) { //am găsit numărul
found = true;
cout<<"DA ";
} else if(x < a[mij]) //x se află în stânga mijlocului, eliminăm a doua jumătate
dr = mij - 1;
else //e implicit că x > a[mij], aşadar eliminăm partea stângă (prima jumătate)
st = mij + 1;
}
if(found == false)
cout<<"NU ";
}
}
Test din căutarea binară
Completează următoarea secvență de cod, fără a adăuga vreun spațiu:
//QUERY este elementul de căutat
int st = 1, dr = n, mij;
bool gasit = false;
while(st <= dr) {
mij = (st + dr) / 2;
if(a[] == QUERY) gasit = true;
...
}Răspunde la următoarea întrebare:
Pentru un şir ordonat crescătora cu n = 210 elemente, în cel mai nefavorabil caz, trebuie făcute comparații.· Vezi răspunsul
Răspunde la următoarea întrebare:
Complexitatea căutării binare este O( n).· Vezi răspunsul
Alte resurse
Am găsit următoarele site-uri sau pagini web ca fiind resurse bune pentru căutarea binară:
Căutarea Binară pe WikipediaCăutarea Binară pe Tutoriale-Pe.NET
Căutarea Binară pe pbInfo
Căutarea Binară pe Infoarena